 <例2>
<例2>
|
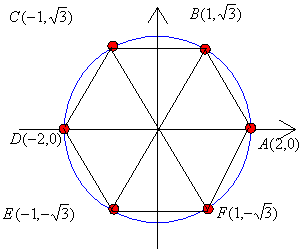
座標平面上の原点Oを中心とする半径2の円に内接する正六角形の頂点を順にA,B,C,D,E,Fとし、Aの座標は(2,0)、Bは第1象現にあるとするとき、 (1)ベクトル 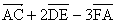 を成分で表すと を成分で表すと である。 である。(2)tを実数とするとき、ベクトル 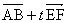 の大きさが最小になるtの値は の大きさが最小になるtの値は で、そのときの最小値は で、そのときの最小値は >である。 >である。
|
(1)求めようとするものが座標と関連したベクトルの成分であるから、これは1次変換によって変化するものである。したがって正六角形を座標で示した(図2)をもとにして解くと良い。(図2)でa=2とおいた場合になるから、
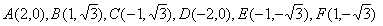
となる。したがって、
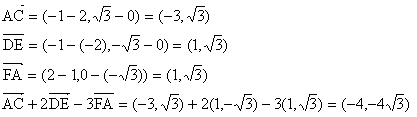
(2)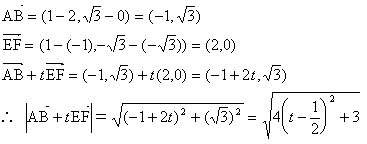
よってt=1/2のとき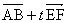 の大きさは最小となり、
最小値は
の大きさは最小となり、
最小値は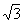 である。
である。