以上のようにして“変身n角形”としての(新図)を求め，この図をもとにして考察してゆくと，正n角形に関するベクトルの問題を比較的簡単に解くことができる。しかも無意識のうちに写像や変換の実例を使いこなしていることになってしまうであろう。それだけでなく，どのような問題が作られ得るか，出題の予想にも役立てることができる。

　【４】の�@により“変身n角形”を簡単に作ることができるような場合は，もとの正n角形にも興味を引く性質があり，従って出題されやすいということになるであろう。

　5，6，8角形については今後もいろいろな形で出題されると思われる。また今後10角形や12角形についても出題の可能性がある。それも“変身n角形”の図から予想されるのである。

　そこで“変身12角形”の図を作ってみよう。【４】のはじめに正8角形を例にして“変身8角形”を求めたように1つ1つ式を立てて求めてもよいし，【４】の�@にあてはめて直接求めてもよい。

その結果は，

　　A₂(+1，1)，A₃(3+，1+)，A₄(3+2，3+)，

　　A₅(4+2，3+2)，A₆(4+2，4+2)，A₇(3+2，4+2)，

　　A₈(3+，3+2)，A₉(1+，3+)，A₁₀(1，1+)

となる。

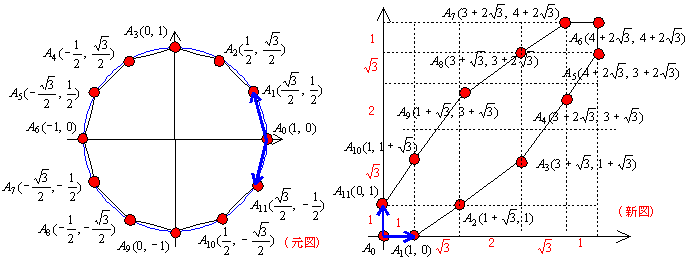
　“変身n角形”の図は変身6角形以外は，数値に無理数が入ってきたりしているがおもしろい性質を持っている。特徴を把んでおけば作図も比較的簡単にできるのである。正12角形の問題を解いてみよう。

（例5）半径1の円に内接する正12角形A0 A1 A2 ･･･A10 A11がある。 　=，=と表わし，A0A2とA1A11の交点をBとする。 (1) 線分A1A11およびA1Bの長さはA1A11=（　　　），A1B＝（　　　）である。 (2) 次のベクトルは， を用いて 　　＝（　　　）+（　　　），　　＝（　　　）+（　　　） 　　＝（　　　）+（　　　） 　である。（立命館大）＝1部改題＝

(1) (元図)で外接円の中心をＯとすると∠A₁OA₁₁=60°であるからA₁A₁₁の長さは半径に等しい。

　　∴　A₁A₁₁=1

　次に(新図)の一部分を下に書いておこう。

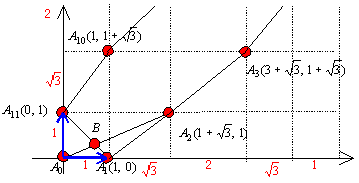
　まずこの(新図)の中でのBの座標を求めておこう。

　　　直線A₀A₂；

　　　直線A₁A₁₁；y=−x+1

　　　交点BはB(−1，2−)

　よってA₁B：A₁A₁₁＝1−(−1)：1＝2−：1

　　∴　A₁B＝(2−)A₁A₁₁＝2−

(2) ＝(−1，2−)＝(−1)(1，0)＋(2−)(0，1)＝(−1) ＋(2−)

　＝(1＋，1)−(1，0)＝(，1)＝+

　＝(3＋，1＋)−(1＋，1)＝(2，)＝2+

　“変身n角形”としての(新図)を作る方法として，1次変換fを表わす行列を求め，そこから各ベクトルの変換を調べてゆく方法もある。

　(元図)での＝(cosθ−1，sinθ)，＝(cosθ−1，−sinθ)がfによってそれぞれ(1，0)と(0，1) に移ってゆくような行列を求める。次にこの行列をもとにして(元図)での＝(coskθ−1，−sinkθ)がどのように移ってゆくかを調べて(新図)でのを決定する。

　この方法によって【４】で述べたことと同じ結果に到達することができる。しかし，ベクトルの関係式を変えない変換ということに着目して考察してきたので行列を意識する必要がなかったのである。