今まで考えてきた1次変換fは基底としてのベクトル![]() =(a1,a2) ,
=(a1,a2) ,![]() =(b1,b2)を新しい基底 (1,0)と(0,1)に変えて行くという働きをする。このfによって正n角形の図(元図)は特殊な形をしたn角形(新図)へと移ってゆく。この(新図)のn角形のことを正n角形の“変身n角形”と呼ぶことにしよう。
=(b1,b2)を新しい基底 (1,0)と(0,1)に変えて行くという働きをする。このfによって正n角形の図(元図)は特殊な形をしたn角形(新図)へと移ってゆく。この(新図)のn角形のことを正n角形の“変身n角形”と呼ぶことにしよう。
“変身6角形”としての(図1)(図2)を初めに考案されたのは札幌予備学院の清水先生である。これにヒントを得て,私も“変身5角形”や“変身8角形”について試みに考え出してみた。それが(図3)(図4)(図5)(図6)である。
ここで“変身6角形”“変身8角形”“変身5角形”については,(図1)から(図6)までに示されている形以外のものも考えられるのか,或いはこれらの図以外にはないのか,また一般に“変身n角形”の図を考案するのは,どのような理論にもとづいて実現されるのか,以上のことについて考察してみよう。
たとえば正8角形A0A1A2A3A4A5A6A7において基底![]() ,
,![]() とした場合,“変身8角形”は(図3)である。この(図3)は(元図)の正8角形の各辺の平行な関係,平行な線分の長さの比等々の関係はずべて保たれている図である。
とした場合,“変身8角形”は(図3)である。この(図3)は(元図)の正8角形の各辺の平行な関係,平行な線分の長さの比等々の関係はずべて保たれている図である。
この図はどのような考えから導き出されるのか。まず正8角形の(元図)として半径1の円に内接する正8角形の図を書いておこう。半径を1に限定したとしても(元図)について論ずる場合の一般性は保たれるからである。
中心を原点OとしてA0を(1,0)にすると他の頂点は右図のようにそれぞれの座標を持つ。
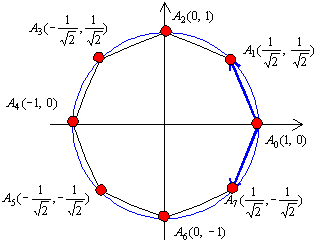
基底のベクトルを成分で表わすと,![]() =(
=(![]() -1,
-1,![]() ),
),![]() =(
=(![]() -1,-
-1,-![]() )となる。
)となる。
次に,![]() ,
,![]() ,・・・
,・・・![]() をこの基底を使って表わしてみよう。
をこの基底を使って表わしてみよう。
![]() =l
=l![]() +m
+m![]() とおくと,
とおくと,
(-1,1)=l(![]() -1,
-1,![]() )+m (
)+m (![]() -1,-
-1,-![]() )
)
∴ (-1,1)= ((![]() -1)(l+m),
-1)(l+m),![]() (l-m))
(l-m))
-1= (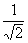 -1)(l+m)・・・(イ),1=
-1)(l+m)・・・(イ),1=![]() (l-m)・・・(ロ) よりl=1+
(l-m)・・・(ロ) よりl=1+![]() ,m=1
,m=1
よって ![]() =(1+
=(1+![]() )
)![]() +
+![]() ・・・(ハ)
・・・(ハ)
この(ハ)は(元図)において成り立つ関係であるが,fによって(ハ)は(新図)においても成り立つ。(新図)はA0が原点で![]() =(1,0),
=(1,0),![]() =(0,1)であるから,(ハ)より(新図)の中での
=(0,1)であるから,(ハ)より(新図)の中での![]() が求められる。
が求められる。
![]() =(1+
=(1+![]() )
)![]() +
+![]() =(1+
=(1+![]() )(1,0)+(0,1)=(1+
)(1,0)+(0,1)=(1+![]() ,1)
,1)
これより(新図)の中でのA2の座標は(1+![]() ,1)である。このようにして(元図)の正8角形におけるベクトルの関係式がすべて保たれているような(新図)を作ってゆくことができるのである。
,1)である。このようにして(元図)の正8角形におけるベクトルの関係式がすべて保たれているような(新図)を作ってゆくことができるのである。
以下同様な計算により
![]() =(2+
=(2+![]() )
) ![]() +(1+
+(1+![]() )
) ![]() 。従ってA3 (2+
。従ってA3 (2+![]() ,1+
,1+![]() )。
)。
![]() =(2+
=(2+![]() )
) ![]() +(2+
+(2+![]() )
) ![]() より,A4 (2+
より,A4 (2+![]() ,2+
,2+![]() )。
)。
![]() =(1+
=(1+![]() )
) ![]() +(2+
+(2+![]() )
) ![]() より,A5 (1+
より,A5 (1+![]() ,2+
,2+![]() )。
)。
![]() =
=![]() +(1+
+(1+![]() )
) ![]() より,A6 (1,1+
より,A6 (1,1+![]() )
)
となり(新図)として(図3)が得られるのである。以上の計算過程から正8角形の図において基底を![]() と
と![]() に選んだ場合は(新図)としての“変身8角形”は(図3)のような場合だけであることがわかる。
に選んだ場合は(新図)としての“変身8角形”は(図3)のような場合だけであることがわかる。
正6角形の“変身6角形”としての(図1)に比べて無理数を含む数値が出てきたりして必ずしも簡単な図とはいえない。これも正8角形の構造に根ざしたものであるからと納得するほかはないであろう。
この“変身8角形”はある種の問題を解くには驚くほどの威力を発揮する。
|
(例4)正8角形ABCDEFGHにおいて,
(1) ベクトル
(2)
(3) |
(新図)として(図3)を用いる。
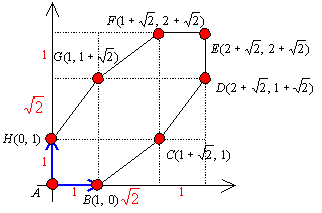
(1) ![]() =(0,1)-(1+
=(0,1)-(1+![]() ,1)=(-1-
,1)=(-1-![]() ,0)=-(1+
,0)=-(1+![]() )
)![]()
![]() =(1+
=(1+![]() ,1)-(1,0)=(
,1)-(1,0)=(![]() ,1)=
,1)=![]() (1,0)+(0,1)=
(1,0)+(0,1)=![]()
![]() +
+![]()
(2) ![]() =(1,1+
=(1,1+![]() )=
)=![]() +(1+
+(1+![]() )
)![]()
![]() =(2+
=(2+![]() ,2+
,2+![]() )=(2+
)=(2+![]() )(1,1)=(2+
)(1,1)=(2+![]() ) (
) (![]() +
+![]() )
)
(3) ![]() =(1,1+
=(1,1+![]() )-(1+
)-(1+![]() ,1)=(-
,1)=(-![]() ,
,![]() )=-
)=-![]() (1,-1)=-
(1,-1)=-![]() (
(![]() -
-![]() )
)
(元図)でもこの関係は成り立つ。(元図)で![]() より,
より,
![]() ∴
∴ 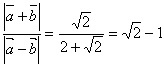
正n角形の“変身n角形”をどの様にして作ってゆけばよいか。(元図)の基底が![]() ,
,![]() の場合で考えてみよう。
の場合で考えてみよう。
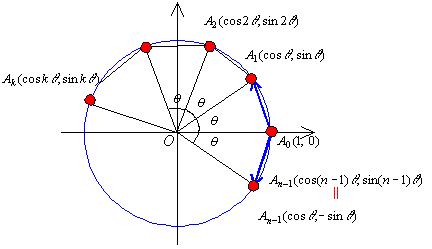
![]() とおくと,外接円の半径を1としてn個の頂点の座標はそれぞれA0(1,0),A1(cosθ,sinθ),A2(cos2θ,sin2θ),A3(cos3θ,sin3θ),・・・,Ak(coskθ,sinkθ)となる。またAn―1(cos(n-1)θ,sin(n-1)θ)であるが,An―1(cosθ,-sinθ)ともなることに注意しよう。
とおくと,外接円の半径を1としてn個の頂点の座標はそれぞれA0(1,0),A1(cosθ,sinθ),A2(cos2θ,sin2θ),A3(cos3θ,sin3θ),・・・,Ak(coskθ,sinkθ)となる。またAn―1(cos(n-1)θ,sin(n-1)θ)であるが,An―1(cosθ,-sinθ)ともなることに注意しよう。
![]() =(cosθ-1,sinθ),
=(cosθ-1,sinθ),![]() =(cosθ-1,-sinθ),
=(cosθ-1,-sinθ),![]() =(coskθ-1,sinkθ)より,
=(coskθ-1,sinkθ)より,![]() =l
=l![]() +m
+m![]() とおく。
とおく。
(coskθ-1,sinkθ) =l(cosθ-1,sinθ)+m(cosθ-1,-sinθ)
=((cosθ-1)(l+m),(sinθ)(l+m))
∴ coskθ-1=(cosθ-1)(l+m), ∴ ![]()
sinkθ=(sinθ)(l+m) ∴![]()
よって ![]() ・・・①を得る。
・・・①を得る。
![]() =l
=l![]() +m
+m![]() は(新図)においても成り立つので(新図)では
は(新図)においても成り立つので(新図)では![]() =(1,0),
=(1,0),![]() =(0,1)となることを考慮すると,
=(0,1)となることを考慮すると,![]() =l(1,0)+m(0,1)より(新図)でのAkの座標が決まる。
=l(1,0)+m(0,1)より(新図)でのAkの座標が決まる。
かくして,![]() となる。
となる。
このようにして次々とA2,A3,・・・,An-2の座標が求められ,(新図)が完成する。以上の計算過程より,このような(新図)はただ1通りの形のものしかありえないことも明らかである。
次に,(元図)の基底が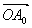 =(1,0),
=(1,0),![]() (cosθ,sinθ)であるときの(新図)を求めてみよう。A0,A1,A2,・・・,Ak,・・・,An-1のそれぞれの座標は前と同じであるから,Ak(coskθ,sinkθ)である。
(cosθ,sinθ)であるときの(新図)を求めてみよう。A0,A1,A2,・・・,Ak,・・・,An-1のそれぞれの座標は前と同じであるから,Ak(coskθ,sinkθ)である。
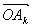 =(coskθ,sinkθ)より,
=(coskθ,sinkθ)より,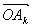 =l
=l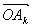 +m
+m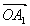 とおいて成分の関係を見る。
とおいて成分の関係を見る。
(coskθ,sinkθ)=l(1,0)+m(cosθ,sinθ)=(l+mcosθ,msinθ)
∴ coskθ=l+mcosθ,sinkθ=msinθ
よって 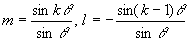 ・・・②
・・・②
以上を利用して(新図)の関係に移ると,
![]() =l
=l![]() +m
+m![]() =l(1,0)+m(0,1)=(l,m)=
=l(1,0)+m(0,1)=(l,m)=![]()
となる。従って,![]() となる。
となる。
またこの計算過程より,この場合の(新図)もただ1通りの形のものしかありえないことも明らかである。