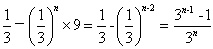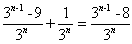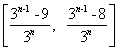(1)G2={[0,1/9],[2/9,1/3],[2/3,7/9],[8/9,1],}
区間の長さ 1/9×4=4/9
(2)GnからGn+1に変化するとき、各区間を3等分して、それぞれの区間の中央から開区間として除くから、
閉区間の個数について、 Gn+1=2Gn
長さの総和について、 Gn+1=2/3・Gn
G1が、閉区間の個数が2個で、長さの総和2/3だから、
Gnについて、閉区間の個数は2n、長さの総和は(2/3)n
(3)G1で得られる、[0,1/3],[2/3,1]において、1/3という点は以後決して取り除かれことがないことに着目すると、閉区間の作り方から求める区間は、[A,1/3]とおける。
ここで、区間の長さの総和は(2/3)n=32/243だから、1区間あたりの長さは、
32/243÷32=1/243、 A=1/3ー1/243=80/243
∴ [80/243,1/3]
(4)Gnは、区間の個数2n個、区間1個の長さは(1/3)n。1番目から2n番目までは、[0,1/3]の中にある。
2n−3番目から1/3まで同じ長さのものは、取り除いた区間と2n−3番目とを含めて9個あるので、2n−3番目の区間の
最初は、 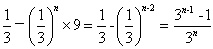
最後は 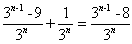
∴ 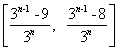
(1)、(2)ともに良くできていたと思う。ただ題意の読みとりに誤解があり、G3をG2に、Gn+1をGnとして解答している生徒がいた。論旨に誤りがなければ半分の得点を与えた。
(3)32÷2=16に気付くかどうかが分かれ道だったと思う。誤答のケ−スは、単純な数列のように扱ってしまった場合が殆どであった。
(4)完答者は8人であった。2倍ずつ区間が増えていくので、数列のように扱えないことを理解して欲しい。この部分は、石黒 悠一朗 君(滝川高校1年)が鮮やかな解答を寄せていました。
解答の「着眼点」で述べたように、「カント−ルの3進集合」と呼ばれるところからの出題でした。3等分して真ん中の区間を取り除いていくという単純な操作が生み出す集合の元は、無限回の繰り返しを仮定すると[0,1]の中の実数と同じだけの個数がある。[0,1]には実数が連続して存在する、したがって区間の長さは1。ところが、3進集合は、中央の長さを取り除いていくので、元を並べて測っても長さは0.感覚的には、「連続体の濃度(元の個数)をもてば長さが0にならない」という感じがするのですが、これを否定する反例になっています。これは、今では無限回の繰り返しを要求する、「フラクタル」、「カオス」の領域でも必ず触れられる概念となっています。
採点して感じたことは、(1)、(2)ですが通常は無限級数を用いて解説がされています。出題者もそれにそって解答を与えました。しかし、解答者の多くの方は、区間の長さを出しどれだけ集めるかという簡潔な方法を採っていました。その柔軟さが羨ましくもあり勉強になりました。都市部、郡部を問わず、発想そのものにそれほどの違いはありませんでした。参加された皆さんの、今後ますますのご健闘を期待してやみません。