ｘ＝２^ｎに対応させてｙとして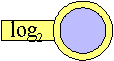のメガネで見える値を書きなさい。

　このような表を２を底とする対数表という。
　対数表を使うと、ｘのかけ算をｌｏｇ_２ どうしの足し算で計算できる。
　このことがコンピュータのない時代の数の計算を簡単にするのに大変役に立ち、天文学者の寿命をのばしたと言われている。

　　ｅｘ．

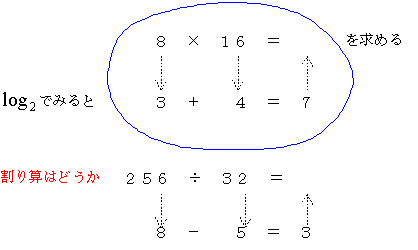
問題　対数表を使って、次の計算をしなさい。

　�@　６４ × ３２

　�A　１６ × １６

　�B　２０４８ ÷ １２８

　�C　５２６ × １／１６

　�D　４ ÷ １／８

　�E　１／２ ÷ １／２

対数の計算規則

　ｌｏｇ_２の対数表で行ったことをｌｏｇ_ａの対数表を使って一般化する。

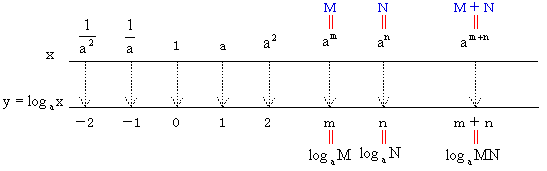
　ａ^２×ａ^３のように真数の掛け算は、対数の足し算に対応している。
　ａ^ｍ×ａ^ｎ＝ａ^ｍ＋ｎのとき、ａ^ｍ＝Ｍ、ａ^ｎ＝Ｎとおくと、

�T　ｌｏｇａＭＮ＝ｌｏｇａＭ+ ｌｏｇａＮ

また、ａ^ｍ÷ａ^ｎ＝ａ^ｍ−ｎだから

�U　ｌｏｇａＭＮ＝ｌｏｇａＭ− ｌｏｇａＮ

また、ｌｏｇ_ａＭ^ｎ＝ｌｏｇ_ａＭ×Ｍ×Ｍ×・・・×Ｍ
　　　　　　　　＝ｌｏｇ_ａＭ＋ｌｏｇ_ａＭ＋・・・＋ｌｏｇ_ａＭ
　　　　　　　　＝ｎｌｏｇ_ａＭ　　だから

�V　ｌｏｇａＭｎ＝ｎｌｏｇａＭ

練習　次の計算をしなさい。

　�@　ｌｏｇ _２ ５１２・６４

　�A　ｌｏｇ _２ １０２４÷３２

　�B　ｌｏｇ _３ ２７・２４３

　�C　ｌｏｇ _２ １６^３