 整数のK進法表示
整数のK進法表示
図のような無造作な正方形の集まりを数で表してみよう。
この場合、必ず10毎にまとめなくてはならないということはないのであり、4毎にまとめる場合や、3毎にまとめる場合等々があってもよいのである。そして「1」を表す正方形が何個か集まって棒状の長方形となり、その棒状の長方形が何個か集まってより大きな正方形が形成されてゆく・・・というのは同じである。3毎にまとめると大きな正方形2枚と、長方形2本と、「1」の正方形1個となりこれを221(3)と表す。この場合の1枚は32であり、1本は3であるから221(3)=2×32+2×3+1=25である。
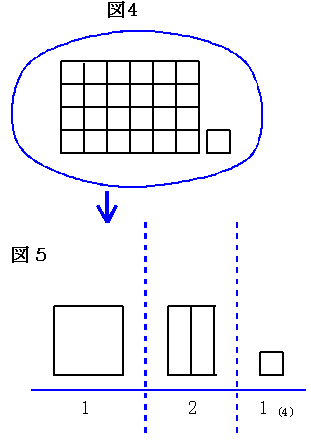
また4毎にまとめると、1枚と2本と1個となりこれを121(4)と表わす。(1図)が次に示す(4図)→(5図)へとまとめられてゆく。
この場合は、1枚は42であり、1本は4を表すから121(4)=1×42+2×4+1=25である。そうして3毎にまとめると3進法、4毎にまとめると4進法による表示といい、一般にK進法による表示が可能である。
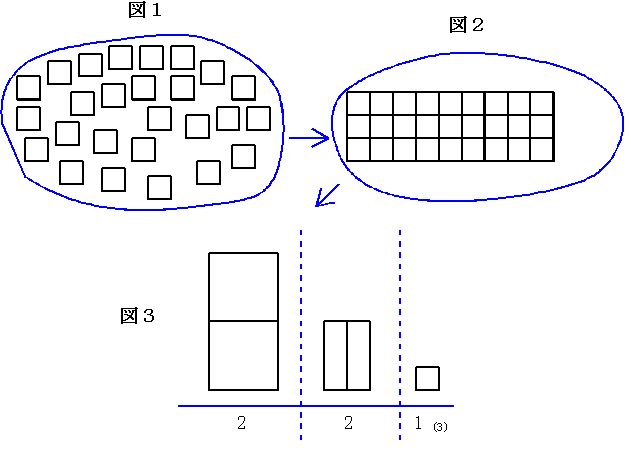
では25を3進法表示すると221(3)となるのは、どのような計算によって求められるのであろうか。前の(1図)から(2図)、(3図)への推移を考察してみよう。これは25個の正方形が8本の長方形と1個の正方形にまとめられたことを示している。あくまでも3毎にまとめるのであるから次のこの8本を3毎にまとめると、大きな正方形2枚と、長方形2本となり、結局は2枚と2本と1個になっている。これを計算の上で考えると、
25=3×8+1 8=3×2+1
というように3で割って商と余りを求め、次にその商を再び3で割って商と余りを求めている。
25=3×8+1=3(3×2+2)+1=2×32+2×3+1である。そこで次のような簡便計算ができる。
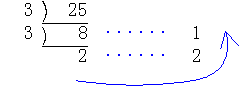
このようにして、25=221(3)として求めることができる。
一般にK毎にまとめる場合も同じように考えてゆくことができる。「1」を表す正方形がK個集まって細長い長方形ができ、これは1本でKを表し、この棒状の長方形がK本集まると大きな正方形となり、これはK2を表している。更にこの大きな正方形をK枚集めると、再び棒状の長方形となり、これはK3を表し、それがK本集まると巨大な正方形が形成されK4を表し・・・となっている。
ここで
Kn,Kn-1,Kn-2,・・・,K,1
を表す図がそれぞれ
a0,a1,a2,・・・,an-1,an
だけある図全体は次のような数を表すことになる。まず
a0a1a2・・・an-1an(K)
=a0Kn+a1Kn-1+a2Kn-2+・・・+an-1K+an
となる。
このとき
a0,a1,a2,・・・,an-1,an
はすべてKより小なる正の整数または0である。何故ならばKn-iの係数aiがもしもKならばKn-iの図が長方形からaiKn-iはより大きな正方形となってしまい、またKn-iが正方形の図ならばaiKn-iはより大きな棒状長方形となり、いずれにしても上の位の数を表す図になってしまうのである。よって、
|
a0a1a2・・・an-1an(K)=a0Kn+a1Kn-1+a2Kn-2+・・・+an-1K+an (a0,a1,a2,・・・,an-1,anはKより小の自然数か0) |
整数NのK進法表示については次の重要な性質がある。整数NをK進法で表すとき、NをKで割り余りと商を求め、ついでこの商をKで割り余りと商を求める・・・というように次々と求められる商と余りが下の通りであったとする。
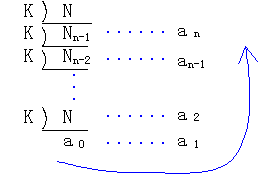
NをKでわると余りanで商がNn-1、このNn-1をKで割ると余りがan-1で商がNn-2・・・とすると
N=a0a1a2・・・an-1an(K)
となる。
そしてこれは一意的に成り立つ。何故ならば次のnこの式はいずれも一意的に成立する。
N=KNn-1+an (0≦an<K)
Nn-1=KNn-2+an-1 (0≦an-1<K)
・・・
N1=KN0+a1 (0≦a1<K かつ 0<a0<K)
そこで
N=KNn-1+an
=K(KNn-2+an-1)+an
=K2(KNn-2+Kan-1)+an
= ・・・
=a0Kn+a1Kn-1+a2Kn-2+・・・+an-1K+an
=a0a1a2・・・an-1an(K)
となりNも一意的に表されるのである。
| (例1)10進法で表された数80をn進法で表すと212となる。nを求めよ。(産業能率大) |
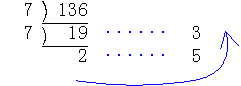
| (例2)136を7進法で表せ。 |