

○分数×分数=分数-分数?
<先 生>
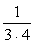 なる分数の面白い性質として、
なる分数の面白い性質として、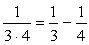
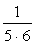 ②
② 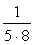
<まなぶ>
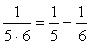 ,②
,② 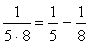 でしょうか。
でしょうか。
<よしお>
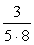 だから左辺と一致しないだろう。
だから左辺と一致しないだろう。
<先 生>
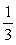 を掛けておく必要がある。従って、
を掛けておく必要がある。従って、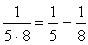 となる。では、いったいどういうときに、単純に積の値が差の値と一致するのだろうか。
となる。では、いったいどういうときに、単純に積の値が差の値と一致するのだろうか。
<かず子>
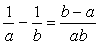
<先 生>
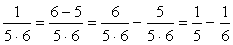
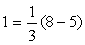
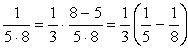
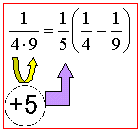 <まなぶ>
<まなぶ>
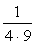 は、分母の差が5だから、
は、分母の差が5だから、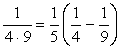
<先 生>
|
ex) 次の数列{an}の初項から第n項までの和を求めよ。 (1) 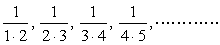 (2) 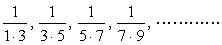 (3) 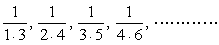 (4) 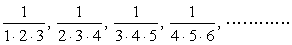 |
<先 生>
<よしお>
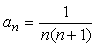
<先 生>
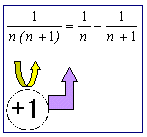 ではこの一般項に対して部分分数分解をしてみようか、かず子。
ではこの一般項に対して部分分数分解をしてみようか、かず子。
<かず子>
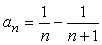
<先 生>
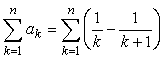

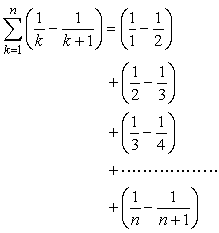
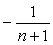 だけだ。結局、
だけだ。結局、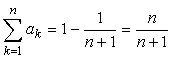
<まなぶ>
<先 生>
<まなぶ>
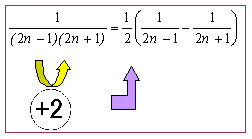 えーと、まずは一般項からですよね。分母の積をみて前の数は、初項1公差2の等差数列より一般項は2n-1、後ろの数はそれより2多いんだから2n+1、だから一般項anは、
えーと、まずは一般項からですよね。分母の積をみて前の数は、初項1公差2の等差数列より一般項は2n-1、後ろの数はそれより2多いんだから2n+1、だから一般項anは、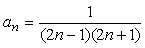
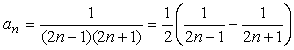

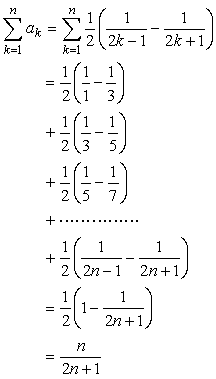
<先 生>
<よしお>
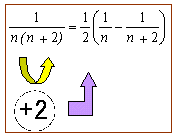 まず一般項は、
まず一般項は、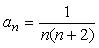
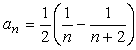
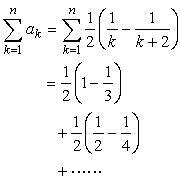
<先 生>
<よしお>
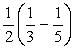 です。
です。
<先 生>
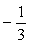 と相殺されそうだね。もう少し頑張って、書きぬいてみよう。
と相殺されそうだね。もう少し頑張って、書きぬいてみよう。
<よしお>
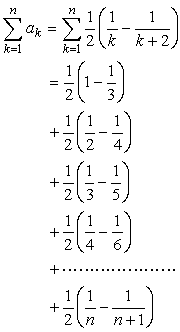
<先 生>
<よしお>

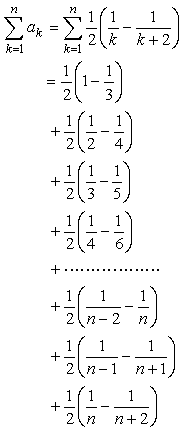
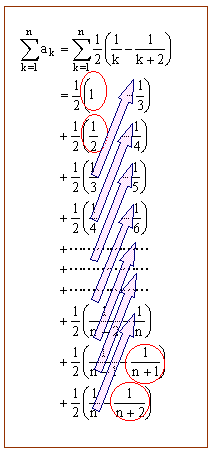 <先 生>
<先 生>
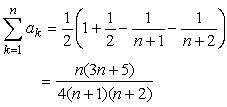
<まなぶ>
<先 生>
<まなぶ>
<先 生>
 次のように、項を2つずつまとめて段を下げていつてみよう。
次のように、項を2つずつまとめて段を下げていつてみよう。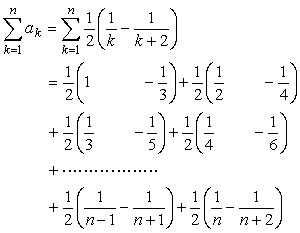
<まなぶ>
<先 生>
<生徒達>
<先 生>
<生徒達>
<かず子>
<よしお>
<かず子>
<先 生>
<かず子>
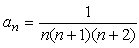
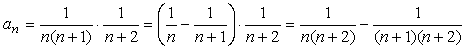
<まなぶ>
<よしお>
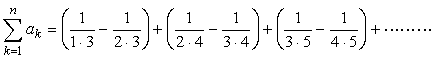
<かず子>
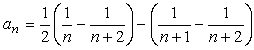
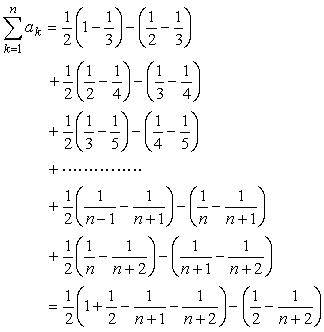
<先 生>
<生徒達>
<まなぶ>
<先 生>
<まなぶ>
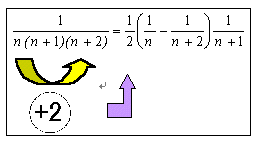 まず、nとn+2はその差が2だから、
まず、nとn+2はその差が2だから、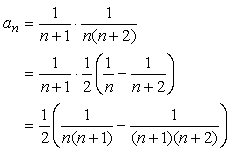
<先 生>
 やってみよう。
やってみよう。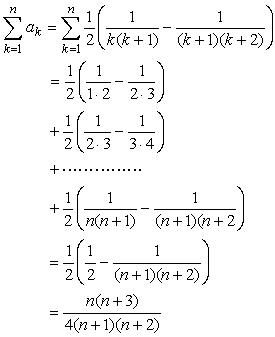
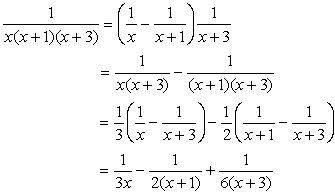
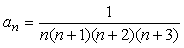
<まなぶ>
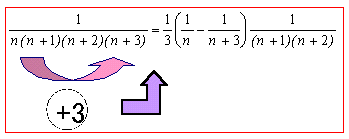 はい、nとn+3の部分で分解します。
はい、nとn+3の部分で分解します。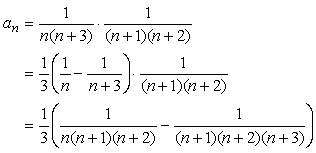
<先 生>
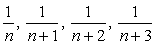 で式が表現されることになる。
で式が表現されることになる。
あとがき
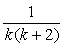 の分解は、
の分解は、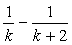 となることを予想し、これを通分します。
となることを予想し、これを通分します。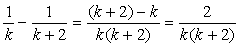
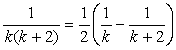
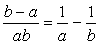
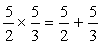
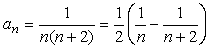 に対して相殺される数を補います。
に対して相殺される数を補います。
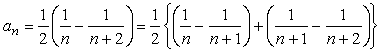
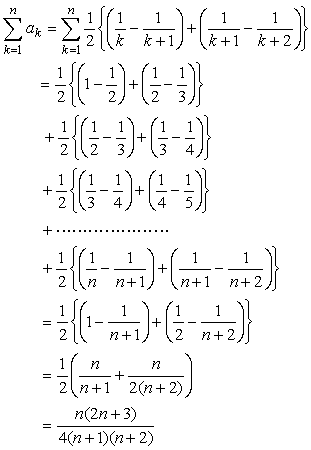
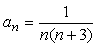 に対しては、
に対しては、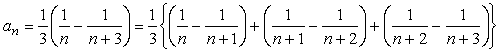
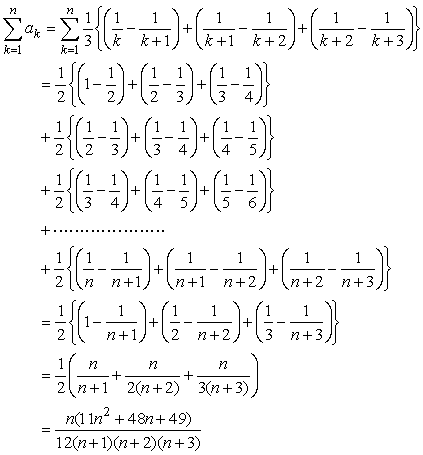
式の見やすさ、まとめやすさを考えるとこのイメージ化がbestと思うのですか。
(4)の部分分数分解も、結果を押し付ける解答が目立つような気がします。しかし、3数の積であろうが4数の積であろうが、その中の2数を選んで逐次分解していくだけのことです。分解のメカニズムを理解をする上でも大事なことではないでしょうか。
なお、次の例は、恒等式の係数決定問題における係数比較法(数値代入法)の定番ですが、部分分数分解を利用した解答も考えることができます(解答の良し悪しは別として)。
ex) 次の式がxについての恒等式であるとき、定数a,b,cの値を求めよ。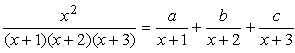
|
解)
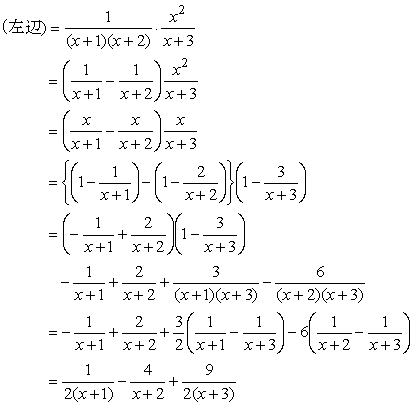
以上より、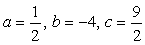
ところで、「小手技シリーズ」はもちろんフィクションですが、その指導の内容についてはノンフィクションの部分もあります。今回の部分分数分解については、本校1年生を対象とした数学A「数列」単元の授業において、実際に指導した内容を脚色したものです。したがって、この小手技は、「指導案」ということになります。