コンパスでグラフを描こう

札幌藻岩高校　中村　文則

【材　料】　本時で使用する素材

コンパスの役目をはたすもの(紐と画鋲、マグネット)

【下ごしらえ】

・紐の端にマグネットや画鋲を結び(貼り)つけておきましょう

【調　理】
《基本編1》　　～角の二等分線をメイクる

菱形の対角線は内角を二等分することを説明。
頂点に紐の端を置き、押さえて、適当な紐の長さの点で２辺を切る。
切った２点から等距離にある点を求める。
菱形の対角線を引く。

※ コンパスでできることをまとめさせよう。

長さがとれる
長さが写せる
点を写せる　　　　　　　etc……

《基本編2》　　　～２次関数のグラフをメイクる

放物線を描く手順の確認
　① 一般形から標準形へ変形
　② 軸の方程式を求める
　③ 頂点の座標を求める
　④ 点をプロットする
　⑤ プロットした点に沿って曲線を滑らか描く

<問題提起>
　プロットするのはどんな点がいいだろうか？　　ワイワイガヤガヤ
　⇒　軸に関して線対称だから、軸の右側か左側のどちらかを描けばいい
　⇒ 両座標軸との交点を求めたほうがいいから、原点のある側
　⇒ 軸の原点側の点をプロットする
　⇒ 反対側は、軸に関して対称点をプロットする
　⇒ コンパスで点を写していこう

【作業工程図】

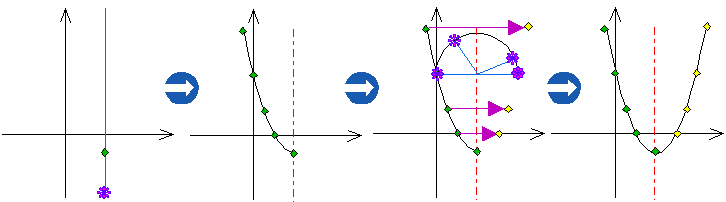
《応用編》　　～３次関数のグラフをメイクる

・３次関数を描く手順の確認
　① 導関数を求める
　② 増減表を作る
　③ 極点(極大値・極小値)を調べる
　④ 点をプロットする
　⑤ プロットした点に沿って曲線を滑らか描く

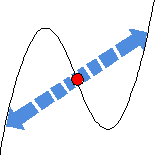<問題提起>
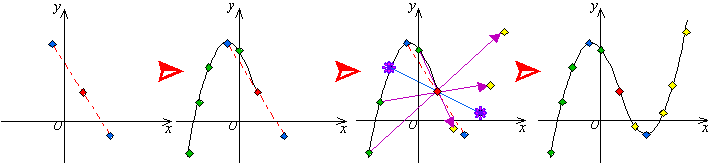
　プロットするのはどんな点がいいだろうか？　　ワイワイガヤガヤ
　⇒　変曲点に関して点対称だから、変曲点の右側か左側のどちらかを描けばいい
　⇒ 両座標軸との交点を求めたほうがいいから、原点のある側
　⇒ 変曲点の原点側の点をプロットする
　⇒ 反対側は、変曲点に関して対称点をプロットする
　⇒ コンパスで点を写していこう

【作業工程図】

まとめ……そして……提案

コンパスを使って放物線のグラフは描こう！
　生徒に放物線を描かせると、もう大変、ぐちゃぐちゃです

折れ線になっている	⇒滑らかに結べんのか!
軸に関して対称でない	⇒バランスってもんがあるだろう！
頂点が鋭利に尖っている	⇒痛いだろ！
グラフが末広がりに外側に開いている	⇒下に凸なら延ばしいていくと墜落するぞ！
グラフがぽつんとある	⇒座標平面いっぱいに描け、ノートがもったいない！
グラフの大きさが分らない	⇒頂点の座標がないと長さの尺度がわからんだろうが！

　一般形から標準形への変形はマニュアル的にできるのに、いざグラフを描かん！、という段で、軸や頂点の意味と意義を見失って、実に安易に点をプロットしてしまうのです。そのため、とんでもないグラフが出現してきます。頂点近くの点を適当にプロットして、座標の値を計算し間違えても全然意に介せず、無理やりにでも線を結ぼうとする。非対称なグラフも彼らにとってはちょっとねじれただけでno problemなのです。
　放物線を二次曲線とみれば焦点の性質から多少安定したグラフも期待できそうですが、あくまで二次関数にこだわって描こうとすると、その性質が希薄になってしまいます。「すべてのグラフは相似である」といった性質はもちろん鋭利な放物線を排除はしてくれますが、グラフを描く上では、もっとも譲れない性質は、軸に対して線対称であるということでしょう。だからこそ、

コンパスを使って放物線のグラフは描こう！
というキャッチフレーズが心の叫びとなってきます。

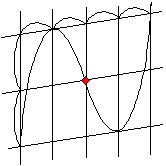　コンパスを使い(対称)軸の片面を、点をプロットして描くと、もう片方も簡単に描かれてしまいます。コンパスを用意できれば一番いいのですが、持っていなくても、「対称点にプロットする」という意識さえあれば、スムーズに鉛筆は動いてくれるでしょう。ほんのちょっとした意識のもちかたでこちらの不満は払拭されるのです。
　３次関数を描くときもまた、コンパス(のようなもの、あるいは意識)が必需品であると思います。
　グラフは変曲点で点対称になりますが、数学Ⅱの分野では変曲点は扱いません。不思議なことであり、納得できないことです。放物線はその対称性から軸や頂点を求めることで、増減表など書かずにグラフの概形が分ります。３次関数も、変曲点と極点を押さえれば増減表は必要ありません。変曲点という単語を使わなくても、「極大点、極小点を結ぶ線分の中点で点対称である」ことをいえば済むことです。その点を基準(中心)に意識してグラフを考え、原点のある側を描けば、片側もスムーズに仕上がるのです。３次関数のもつ変曲点、曲点および接線に関する右図の美しい性質は、声高らかに主張されるべきではないでしょうか。形が分らぬグラフを予想できるからこそ増減表の存在価値はあるのです。
　しかし、教科書ではひたすら、ひたすら、増減表から三次関数のグラフを書くことを要求し続けます。性質という結論をださずに要求し続けるのです。そして、生徒も増減表こそがグラフを描く無二無三の方法として、ひたすらひたすら悲しいかな、描き続けるのです。

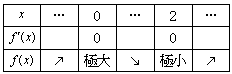　だから、私はいつもささやかな抵抗をします。例えば y=x³-3x²+2 のグラフなら、３次の項の係数からグラフの概形を予測させます。
　そのあと、f'(x)=0 となる点を求め、増減表の一段目を埋めます。
　次に、三段目の矢印を先に書かせてから、二段目の符号をいれて、増減表を完成させてしまいます。ところが、生徒はその方法に慣れてくると、私以上にもっとシビアな抵抗をしてきます。彼らは、二段目の符号を書くのを忘れてしまうのです。